競艇場固有のレースを統計的に分類しようとしてみた

2019年12月12日2019年12月25日競艇, 統計

固有のレースとは？

固有のレースとは、上画像のように、各競艇場で組まれているオリジナルな名前を持ったレースを指します。

各枠番に固定したグレードの選手を配置して、配当や予想の難しさの面で番組を盛り上げようとする試みです。

ただ、このように偏ったレースとなると、競艇場別の平均連対率を出すときなどに、通常の分布からかけ離れているため困るのです。

例えば、インが強い場が統計的に分かったとしても、それは一号艇に毎回A1選手が置かれているだけだとしたら、インが強い場という事にはなりません。

固有のレースを特定したい理由は、競艇場の特徴を分析する際に邪魔になるから、です。

先に結論

先に結論から言います。

以上！！…

ではなく、順を追って解説したいと思います。※うまいアイデアをお持ちの方、コメントください。。

分析手法

正直、公式HPを直接目で見て確認していった方が確実で早い気もしますが、敢えて統計的に処理してみます

（ただの面倒くさがりとも言えます…）。

なお、ここで紹介する手法は私のいちアイデアに過ぎないので、正しさの保証はありません。

※統計的な手法としての正しさではなく、固有のレースを分類する手法の正しさ（適当さ）に関してです。

固有のレースを分類するのに、統計的仮説検定を用います。

統計的仮説検定

なにやら難しそうな言葉ですが、これが意味するところは次の通りです。

統計的仮説検定においては、仮説が正しいと仮定した上で、それに従う母集団から、実際に観察された標本が抽出される確率を求め、その値により判断を行う。その確率が十分に（予め決めておいた値より）小さければ、その仮説を棄却する（すなわち仮説は成り立ちそうもないと判断する）。

wikipedia

母集団と標本については、実際に説明する過程で、どのデータがそれらに当たるのかを説明します。

どういった仮説を立てるか

固有のレースというのは、選手の強さ（グレード）に偏りがあります。その偏りが、普通と比べて明らかに違っていれば、それは固有のレースと呼べるでしょう。

ここでの仮設とは、普通の分布（母集団）と固有のレースの分布（標本）は同じ分布である！　という仮設です。

統計の検定って少し分かりにくいのですが、発想が逆なんですよね。違う事を検定するのは、同じである事を仮定します。

その仮設のもと、母集団が標本をどれだけの確率（p値という）で再現できるか、という事を検定します。

では、その母集団と標本は具体的に何に当たるでしょうか？

母集団（普通）と標本の定義

単純には、各枠番にはA1,A2,B1,B2のどれかの選手が入るわけですから、競艇場関係なく全ての枠番でどのグレードの選手が選ばれているのかを集計してやります。

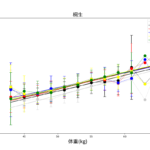
するとこうなります。

わかりづらいですが、ヒストグラム化するためにグレードをB2→1, B1→2, A2→3, A1→4 という数字に置き換えたので、読み替えてください。

こうして見ると、かなり偏りがありますね。特に驚くのが、１号艇のA1選手の多い事。

これじゃあ、そりゃインが強いってなりますよね笑

逆に固有レースの分布はどうなるかというと、まあかなり偏るわけですね。

• 

• 

• 

• 

• 

• 

このように偏ったレースを検定したいので、このようにレース名称毎に括った分布を標本とします。

ただ、SGやG1になるとほぼ全員A1選手ですよね？　それが普通じゃないのかというと、明らかに普通なので、そこも区別します。

さらに、明らかな固有レース分布が反映するのも普通ではない（※とはいえ競艇場全部に渡って足しあげたら平均化されると思っていたがそうならなかったので、やはり上記固有レースっぽいものは省きたい）ので、

各グレード別＋「一般」or「一般戦」or「予選」の名が付くレースでグループ化したものを普通と定義します。

すると一般戦（G1やSGではない）ではこうなります。

この分布を、普通とします。つまり、母集団に当たります。

ここで注意すべき点は、この母集団はあくまで私が定義はしたものです。なので、この検定での分類全てにおける前提条件となります。（一般的な母集団は分からないので、こう置いて考えましょう、という事）

まとめると、母集団はレースグレード毎に三つ定義します。

グレード	レース名称
SG,PG1,G1	一般 or 一般戦 or 予選
G2,G3	一般 or 一般戦 or 予選
一般戦	一般 or 一般戦 or 予選

検定手法

コルモゴロフ–スミルノフ(KS)検定を使います。

詳しい説明は省きます（できない）が、要は、母集団と標本の累積確率を端からプロットしていったときに、その標本が描く曲線が母集団の曲線に対して尤度がどんだけか、というのをやっている（のだと勝手に思っている）んです。

上述しましたが、検定を行うとp値(0〜1の値をとる)を得ます。

仮設では、母集団と標本が同じである事を仮定しているので、p値が1に近いほど母集団の分布に近く、0に近いほど母集団の分布とは異なる、ということです。

python は便利なもので、このKS検定がライブラリ化されており、簡単にできます（良いまとめサイトをのせておきます。こことここ）。

結果

さて、検定した結果から固有のレースをバーンっとお見せしたかったのですが、冒頭でも言ったようにうまくいきませんでした…。

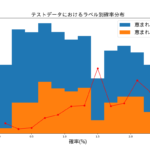
何を条件に固有レースと判断するのかが難しいです。というのも、次の結果を見てください。

うまくいかない例①

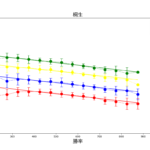
蒲郡競艇場の一般戦の分布です。

赤丸で囲ったところは、図1の"普通"分布と少しずれています。

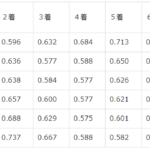
標本の統計量は比較的十分なので、p値としては下記となりました。

１号艇	3.68e-20
２号艇	3.41e-25
３号艇	7.02e-16
４号艇	0.0449
５号艇	0.466
６号艇	2.66e-09

分布の形はそこまでずれているわけではないので個人的には受容したいのですが、検定結果は容赦のないp値でした。

とはいえやはり、統計的には母集団からずれているのでしょう。

ここで、５号艇の分布は、有意水準を0.01%とすると分布は母集団と同じといえるので、つまり普通と言えます。

そこで、固有レース（というより普通の分布ではないレース）の条件を、全ての枠番が有意水準0.01%を下回っている事、とします。

その条件で検証したのですが…

うまくいかない例②

芦屋の場合、「一般」も「予選」も分布が異なりました。

芦屋だけでなく、他の競艇場もいろいろ引っかかりました。

• 

• 

図1と比較してもらうと一目瞭然ですが、全く違います。一号艇のA2以上の比率がおかしいです。

繰り返しますが、「予選」や「一般」の名称と一致するレースでの分布でこうなのです。

結論として、いくらレースグレード別で分けようが

つまり、競艇場全体の母集団を定義しましたが、それには無理があったということなんです。

悪あがき

選手グレードがB2〜A1（１〜４）の絶対値で分布をとっているのが良くないかなと思い、各レース毎の平均値からの相対値（下記表のような計算）での分布で検定もしてみました。

今回の目的は、この検定の先にある競艇場毎の特徴（インが勝ちやすい）を見つける事なので、選手グレードが偏っていても、レース単位での強さのバランスが同じであれば問題ない、と考えたのです、

枠番	級	数値	レースでの平均	相対値
１号艇	A1	4	2.333	1.666
２号艇	B1	2	2.333	-0.333
３号艇	B1	2	2.333	-0.333
４号艇	A2	3	2.333	0.666
５号艇	B1	2	2.333	-0.333
６号艇	B2	1	2.333	-1.333

しかし、結果はあまり変わらずで、こちらの検証方法も使えませんでした…。

まとめ

長くなりましたが、上述したように、仮設検定での分類はうまくいきませんでした。母集団の仮定が間違っているのか、その後の検定方法が間違っているのか…。いずれにしてもいつかリベンジしたいです。では