機械学習を使ってモーター性能を数値化し超抜モーターを探索する

2020年2月29日2020年3月5日機械学習, 競艇

はじめに

競艇番組などで展示を見た解説者が「６号艇のモーターの回り足が良いですよね」など『出足』『伸び足』『回り足』といった表現でモーターの良し悪しをコメントしているのをよく見ますが、私はあれが本当に分かりません。

周回展示を"目"で見て何を判断根拠としているのかも分かりませんし、それが定量的・もしくは定性的に評価されているわけでもなく、モーターの評価というのは、完全に各個人が学習した個人の判断基準に基づく評価と言えるでしょう。

別にそれを批判しているわけではなく、私には真似できないと言いたいのです。では私なりのモーターの評価はどうすべきか。

そう、機械学習なんですね。

しかし難しいのが、モーター性能に関わる数値データが得にくい、という事です。公式HPや配布テキストの情報を見ても、モーター性能に直接関わるデータは展示タイム、ぐらいではないでしょうか。

周回展示の他の数値情報ほしいですよね。野望としては、レース動画を学習させてモーターに関わらず競艇の様々な特徴を動画から導きたいとことはありますが、それはいつの事になるやら分かりません。

ひとまず、現状得られる数値データをもとに分析してみましょう。

モデルの指針

モーターの状態が良いと何が良くなるのか。そう、着順です。

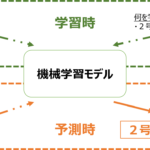
なので、モーターの様々な特徴量だけから、着順を学習してみることにします。

しかし、着順は枠番も関係あるし、何より下手な選手が良いモーターを使っても良い成績にはならない、と言えるでしょう。そのため、枠番と選手の強さに関する依存をできるだけ排除します。

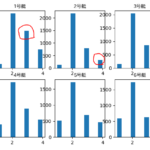
具体的には各選手毎の枠番別平均着順を計算しておき、各枠番毎に実際の着順からその平均着順を引いた値を計算します。具体的には６枠分の計算としては以下となります。

枠番	計算方法
１号艇	着順結果　ー　選手別１号艇時平均着順
２号艇	着順結果　ー　選手別２号艇時平均着順
３号艇	着順結果　ー　選手別３号艇時平均着順
４号艇	着順結果　ー　選手別４号艇時平均着順
５号艇	着順結果　ー　選手別５号艇時平均着順
６号艇	着順結果　ー　選手別６号艇時平均着順

ここでの「平均着順」は、全国の場での１年間の平均着順とします。

この計算方法で計算して得られた値はモーターの状態に依存する「着順変動期待値」とでも呼べる値になっているでしょう。この値を正解ラベルとして機械学習します。

モデル概要

アルゴリズムやらデータ量は下記になります。

アルゴリズム	LightGBM
モデルタイプ	回帰
特徴量	209 ※当日のあらゆるデータ(天気や展示等)は使用していない
訓練データ	1437062(2015〜2019前期)
評価データ	160853(2019後期)

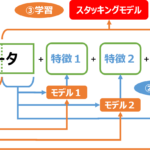
他の着順予想のモデルなどでは１レース１レコードでデータ作成していますが、このモーター数値化モデルでは１レースで６レコードのデータを作成します。

また、学習データに関しては転覆やスタート事故等でゴールできていない艇は省いています。

評価

評価が本当に難しいです。

そもそも正解ラベルとした値が自分で決めた指標のため、その指標が一般的にどこまで正しいのかを評価できていない以上、機械学習の評価値を出したところであまり意味がありません。

とりあえず評価値を載せておきます。

決定係数	0.015
RMSE	1.453
MAE	1.194

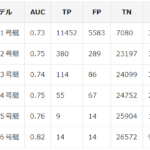
方向が逆ですが、機械学習で得られたスコアがどれだけ使えるのかを評価したいと思います。例えば、各競艇場でのモーター評価がありますが、それと比較してみます。

難しいことは、各競艇場のモーター評価の正しさも保証されない（何度も言いますが批判しているわけではなく、数値化されていない（※公表されていない）ためです…）のと、公式サイトのモーター評価は本サイトで用いている以上の特徴を使って判断している点で真似できない、という事です。

SGレースでは特設サイトが設けられてモーターの機力評価が書かれているので、それと比較してみることにします。

モーター性能の偏差値化

比較の前に、現状のスコアでは数値だけ見ても判断が難しいため、スコアを偏差値化します。

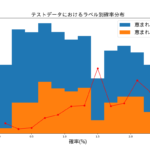
偏差値化する前に、正解ラベルと予測値のヒストグラムを見てみます。

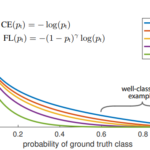
見てわかる通りだいぶ分布の差があります。アルゴリズムの損失関数はRMSEです（公式HPのobjective=’regression’）。

これを見ると本当に学習できてんのか、と思いたいのですが、RMSEを損失関数にするとこういった分布になるのもいた仕方ないのかなとも思ってしまいます。

予測値の方はガウス分布になっているので、この分布に基づいて偏差値化します。

SGの特設サイトとの比較

訓練されていない期間が2019年7月以降なので、その期間に開催されたSGを対象にします。では、表にしていきましょう。

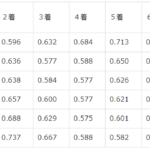
	第２４回オーシャンカップ　公式	機器学習モデル偏差値
1位	３５号機	57.6
2位	４５号機	54.0
3位	１６号機	57.1
4位	５７号機	66.8
5位	７号機	65.4
6位	５９号機	54.5

※↑偏差値の分布で５５以上は少なかったので、相対的に見ると公式評価と概ね一致している。

	第６５回ボートレースメモリアル　公式	機器学習モデル偏差値
1位	３４号機	61.8
2位	２５号機	45.1
3位	１２号機	48.8
4位	４９号機	64.9
5位	７６号機	46.4
6位	２８号機	57.6

※↑一致していない。言い訳として、公式評価が二連対順だったのが気になった。

	第６６回ボートレースダービー　公式	機器学習モデル偏差値
1位	４２号機	61.5
2位	２４号機	48.3
3位	１５号機	72.4
ー	６６号機	44.1
ー	７２号機	64.2

※↑２４号機は中間整備が関わってるみたいなのでこれを評価するのは不可能。それ以外は概ねOK

	第２２回チャレンジカップ　公式	機器学習モデル偏差値
ー	２９号機	75.9
ー	３７号機	77.2
ー	１１号機	64.7
ー	２４号機	66.4
ー	３３号機	49.9
ー	２７号機	54.5

※↑◎が２つ以上ついているモーターをピックアップ。上位は一致。

	第３４回グランプリ／グランプリＳ　公式	機器学習モデル偏差値
ー	８８号機	75.4
ー	７８号機	58.3
ー	１７号機	47.4

※↑◎が２つ以上ついているモーターをピックアップ。うーん・・・。

とりあえず評価してみたのですが、なんとも言えませんね。公式HPの評価も二連対順になっているのもありましたし、「出足」「伸び足」「回り足」の◎の数でピックアップしましたが、◎の数で評価するのも違う気がしますし（ひとつの◎でも強烈なモーターかもしれない）。

また、競艇場によって偏差値の分布に差が出ている気がします。モーターの機力が活かしやすい場と活かしにくい場があるとすると、全体の分布で偏差値をとるのは正しくないかもしれません（活かしやすさも含んだ偏差値が出せるメリットはあるが）。そこは考慮できていませんでした。

つまり、偏差値については、ふーん、まあ参考にしてあげなくもないよ、といった程度と思ってください笑

まとめ

モーターの機械学習モデルを作成してモーターの良悪を数値化してみました。ポイントとしては下記にまとめます。改良点として、アルゴリズムの損失関数をRMSEとしたのは微妙かなと感じています。もっと適した損失関数がありそうです。

また、モーターを数値化する上での着眼点（正解ラベル）は概ね正しいと思っていますが、その評価については難しい事がわかりました。より良い評価について継続して考えてみます。